안녕하세요. 개발자 Jindory입니다.
오늘은 컴퓨터가 실수를 표현하는 방법과 실수 연산시 주의사항에 대해서 알아보고자 합니다.
# 글 작성 이유
Java에서 0.1+0.2가 0. 30000000000000004가 나오는 이유에 대해서 알아보고 어떻게 정확한 방법으로 연산할 수 있을지에 대해서 알아보고자 합니다.
숫자의 표현 방법
일상생활에서 사람이 숫자를 표현 할 때 2와 9.625처럼 10진수를 사용하여 표현합니다. 아마도 손가락이 10개인 생리적 특성 때문에 10진법이 숫자를 세는 기본 단위가 된것 같습니다. 이와는 다르게 컴퓨터는 전기 신호로 정보를 처리하기 때문에 에 디지털 신호인 0과 1을 통해 2진법으로 데이터를 처리 및 관리합니다.
그래서 위 숫자들을 2진법으로 변환하면 2는 10(2) 9.625는 101.101(2)로 표현합니다.
컴퓨터가 실수를 표현하는 방법
컴퓨터가 실수를 표현하는 방법에는 주로 고정 소수점 방식과 부동 소수점 방식이 있습니다.
- 고정 소수점- 이 방식은 소수점의 위치를 고정하고, 정수부와 소수부를 나눠서 표현합니다.- 예를 들어 32비트 컴퓨터가 16비트씩 나누어 실수를 고정 소수점 방식으로 표현한다면 첫번째 비트는 부호를 나타내고, 그 다음의 일부 비트는 정수를 표현하며, 나머지 비트는 소수를 표현합니다.
- 이 방식은 정수 부분과 소수 부분의 자릿수가 한정되어 있어 표현할 수 있는 범위가 제한적일 수 있습니다.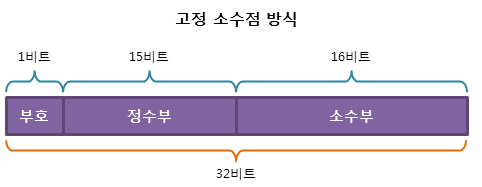
- 부동 소수점
- 이 방식은 소수점의 위치를 고정하지 않고, 실수를 과학적 표기법으로 표현합니다.
- 부동 소수점 수는 부호 비트,지수 부분, 가수 부분의 세 부분으로 나눕니다.
- 부호 비트는 양수인지 음수인지를 나타내고, 지수 부분은 소수점의 위치를 나타내며, 가수 부분은 유효 자릿수를 나타냅니다.
- 이 방식은 소수점의 위치가 유동적이므로 수의 크기에 따라 소수점의 위치를 변경할 수 있고, 그만큼 많은 수를 표현할 수 있습니다.

IEEE 754 부동소수점 표현 방법
초기에는 부동소수점을 표현하기 위하여 컴퓨터 마다 여러가지 서로 다른 형식으로 사용하였으나, 현재는 거의 대부분의 컴퓨터들이 호환성을 위해 미국 전기전자공학회(IEEE)에서 표준화한 IEEE 754 형식을 사용하고 있습니다.
IEE 754 부동 소수점 표현에서 숫자는 아래와 같이 부호부, 지수부, 가수부의 세 부분으로 구성됩니다.
각 부분의 역할과 사용하는 비트 수는 아래와 같습니다.

부호부(Sign) : 숫자의 부호를 나타내며, 양수일 때 0, 음수일 때 1이 됩니다.
지수부(Esponent bit) : 지수를 나타냅니다.
가수부(Fraction bits or Mantissa) : 유효숫자를 나타냅니다.

위 그림은 32비트(4바이트)를 사용하는 방식의 단일 정밀도(Single precision)와 64비트(8바이트)를 사용하는 배 정밀도(Double precision)의 부호부,지수부,가수부의 비트 범위 입니다.
단일 정밀도와 배 정밀도를 구분한 이유는 표현할 수 있는 수의 범위와 정밀도를 조절하기 위함입니다.
단 정밀도는(Single Precision)는 32비트를 사용하며, 1개의 부호비트, 8개의 지수비트, 23개의 가수비트로 구성되어 있습니다. 이 형식은 배정밀도에 비해 더 적은 메모리를 사용하지만, 표현할 수 있는 수의 범위와 정밀도가 제한적입니다.
배 정밀도(Double Precision)은 64비트를 사용하며, 1개의 부호비트, 11개의 지수비트, 52개의 가수비트로 구성되어 있습니다. 이 형식은 단 정밀도에 비해 더 많은 메모리를 사용하지만, 표현할 수 있는 수의 범위와 정밀도가 더 큽니다.
따라서 메모리 사용량과 정밀도 중 중요성에 따라서 단 정밀도와 배 정밀도 표현 방법 중 하나를 선택하여 표현하면 될것 같습니다.
부동소수점 변환 방법
숫자 -23.625를 IEEE 754 부동소수점 방식으로 표현하는 방법에 대해서 알아보도록 하겠습니다.
< 단정밀도로 부동소수점 나타내는 방법 >
- 총 32비트를 0으로 표현합니다.
0000 0000 0000 0000 0000 0000 0000 0000 - 32비트를 부호부, 지수부, 가수부로 나눕니다.
0(1,부호부) 0000 0000(8,지수부) 000 0000 0000 0000 0000 0000(23,가수부) - 제시된 숫자는 음수이므로 부호부를 1로 바꿉니다.
1(1,부호부) 0000 0000(8,지수부) 000 0000 0000 0000 0000 0000(23,가수부) - 정수부분과 소수부분을 2진법으로 변경합니다.
00010111(23) . 101(0.625) - 맨 왼쪽에 1이 하나만 존재하도록 우측으로 시프트 연산을 합니다.
10111.101 -> 1.0111101 * 2^4
이러한 과정을 통해 만들어진 수를 정규화된 부동소수점 수라고 합니다. - 정규화된 부동소수점 수를 기준으로 지수부와 가수부를 만듭니다.
- 지수부 만들기
- 지수부는 이전에 정규화된 부동소수점 수를 만들기 위해 시프트 연산을 한 횟수를 기준으로 합니다.
- 총 4번의 시프트 연산을 하였으므로, 4를 넣을 것입니다.
- 그런데 그냥 4을 넣는것이 아니라 bias값 127을 추가해야 합니다.
- 우측으로 Shift하면 양수, 왼쪽으로 Shift하면 음수가 되므로 양수와 음수를 모두 표현 가능하게 하기 위해 bias값을 더합니다.
- 값 비교 혹은 무한대, NaN과 같은 특수한 값을 편하게 다루기 위해서 bias가 사용됩니다.
- 4 + 127 즉, 131을 지수부에 넣으면 됩니다.
- 최종적으로 1000 0011가 지수부가 됩니다.
- 가수부 만들기
- 가수부는 정규화된 부동소수점 수의 소수점 이하 숫자 뒤에 0을 덧붙여서 총 23비트를 만들면 됩니다.
- 정규화된 부동소수점 수 011 1101에 나머지 16개의 0을 붙혀서 아래와 같이 만듭니다.
011 1101 0000 0000 0000 0000
- 지수부 만들기
- 최종적으로 -23.625를 IEEE 754의 단정밀로 방법으로 표현하면, 1(1비트,부호) 1000 0011(8비트,지수부) 011 1101 0000 0000 0000 0000(23비트, 가수부) 가 됩니다.
< 배 정밀도로 부동소수점 나타내는 방법 >
- 총 64비트를 0으로 표현합니다.
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 - 64비트를 부호부, 지수부, 가수부로 나눕니다.
0(1,부호부) 000 0000 0000(11,지수부) 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000(52,가수부) - 제시된 숫자는 음수이므로 부호부를 1로 바꿉니다.
1(1,부호부) 000 0000 0000(11,지수부) 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000(52,가수부) - 정수부분과 소수부분을 2진법으로 변경합니다.
00010111(23) . 101(0.625) - 맨 왼쪽에 1이 하나만 존재하도록 우측으로 시프트 연산을 합니다.
10111.101 -> 1.0111101 * 2^4
이러한 과정을 통해 만들어진 수를 정규화된 부동소수점 수라고 합니다. - 정규화된 부동소수점 수를 기준으로 지수부와 가수부를 만듭니다.
- 지수부 만들기
- 지수부는 이전에 정규화된 부동소수점 수를 만들기 위해 시프트 연산을 한 횟수를 기준으로 합니다.
- 총 4번의 시프트 연산을 하였으므로, 4를 넣을 것입니다.
- 그런데 그냥 4을 넣는것이 아니라 bias값 1023을 추가해야 합니다.
- 우측으로 Shift하면 양수, 왼쪽으로 Shift하면 음수가 되므로 양수와 음수를 모두 표현 가능하게 하기 위해 bias값을 더합니다.
- 값 비교혹은 무한대, NaN과 같은 특수한 값을 편하게 다루기 위해서 bias가 사용됩니다.
- 4 + 1023 즉, 1027을 지수부에 넣으면 됩니다.
- 최종적으로 100 0000 0011가 지수부가 됩니다.
- 가수부 만들기
- 가수부는 정규화된 부동소수점 수의 소수점 이하 숫자 뒤에 0을 덧붙여서 총 52비트를 만들면 됩니다.
- 정규화된 부동소수점 수 0111 1010에 나머지 16개의 0을 붙혀서 아래와 같이 만듭니다.
0111 1010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
- 지수부 만들기
- 최종적으로 -23.625를 IEEE 754의 배정밀로 방법으로 표현하면, 1(1비트,부호) 100 0000 0011 (11비트,지수부) 0111 1010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 (52비트, 가수부) 가 됩니다.
0.1과 0.2를 더한 값에 오차가 생기는 이유
그렇다면 컴퓨터가 실수를 계산할때 오차가 생기는 이유는 무엇 때문일까요?
그것은 실수를 표현하는 고정 소수점 방식과 부동소수점 방식에서 근사치 값을 사용하기 때문입니다.
10진수 0.1과 0.2를 컴퓨터로 계산한다고 가정하겠습니다.
0.1을 2진수로 변경하면 0.0001 1001 1001 1001 1001 1001 ....로 무한 소수로 표현됩니다.
0.2를 2진수로 변경하면 0.0011 0011 0011 0011 0011 0011 ....로 무한 소수로 표현됩니다.
둘을 합산하면
0.0100 1100 1100 1100 1100 1100...가 결과로 나옵니다.
이 이진수를 10진수로 바꿔보면 대략 0.3000000000000000437114가 나오게 됩니다.
결과적으로 2진수로 바꿨을때 순환소수로 표현되어 어쩔수 없이 정확한 10진수로 변환할 수 없어서 그렇습니다.
0.1과 0.2를 더한 값을 오차없이 계산하는 방법
그렇다면 10진수 0.1과 0.2의 합산을 오차없이 계산하는 방법은 무엇이 있을까요?
한가지 방법으로 Java의 BigDecimal 자료형을 사용하면 됩니다.
BigDecimal은 불변의 임의 정밀도의 부호가 있는 자료형 입니다.
BiDecimal 자료형은 정밀도의 손실 없이 모든 숫자를 처리할 수 있는 자료형입니다.
이는 BigDecimal 내부적으로 수를 저장할 때 이진수의 근사치를 사용하지 않기 때문입니다.
import java.math.BigDecimal;
public class Main {
public static void main(String[] args) {
BigDecimal a = new BigDecimal("0.1");
BigDecimal b = new BigDecimal("0.2");
BigDecimal sum = a.add(b);
System.out.println(sum);
}
}그러나 BigDecimal은 기본적으로 16바이트 이상의 메모리를 차지하며, 객체 생성과 메모리 사용, 연산의 복잡성의 이유로 float, double보다 성능적인 면에서 느릴 수 있습니다.
이렇게 컴퓨터가 실수를 표현하는 방식과 실수 계산시 주의사항에 대해서 알아봤습니다.
혹시라도 정정할 내용이나 추가적으로 필요하신 정보가 있다면 댓글 남겨주시면 감사하겠습니다.
오늘도 Jindory 블로그에 방문해주셔서 감사합니다.
[ 참고 ]
한 권으로 읽는 컴퓨터 구조와 프로그래밍
2진수의 실수 표현 방법 - 고정소수점과 부동소수점, IEEE 754, BCD 등 : 네이버 블로그 (naver.com)
https://jake-seo-dev.tistory.com/428
https://codetorial.net/articles/floating_point.html
숫자를 부동소수점 방식으로 표현하기 - Codetorial
부호, 지수, 가수 IEEE 754 부동소수점 표현에서 숫자는 아래와 같이 부호부, 지수부, 가수부의 세 부분으로 구성됩니다. 각 부분의 역할과 사용하는 비트 수는 아래와 같습니다. 부호부 (Sign) : 1비
codetorial.net
'개발 > Java' 카테고리의 다른 글
| [JAVA] static에 관하여 (0) | 2023.12.13 |
|---|---|
| [JAVA] JVM 메모리 구조 (0) | 2023.12.13 |
| [Java] LocalDate,LocalTime,LocalDateTime 활용하기 (0) | 2022.11.02 |
| [Java] Windows 환경에서 jdk버전 2개 이상 관리 (0) | 2022.09.26 |
| [Java] Collection Framework(List,Set,Map) (0) | 2022.04.17 |
![[Java] 컴퓨터가 실수를 표현하는 방법과 실수 연산시 주의사항(IEEE 754)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FLkoko%2FbtsBJhFt3wf%2FJhH8jfrI4fl35HbOIjZqYk%2Fimg.png)